Understanding Unimodal Bias in Multimodal Deep Linear Networks ICML 2024

Yedi Zhang1	Peter Latham1	Andrew Saxe1,2

1: Gatsby Computational Neuroscience Unit, University College London
2: Sainsbury Wellcome Centre, University College London

---

Abstract

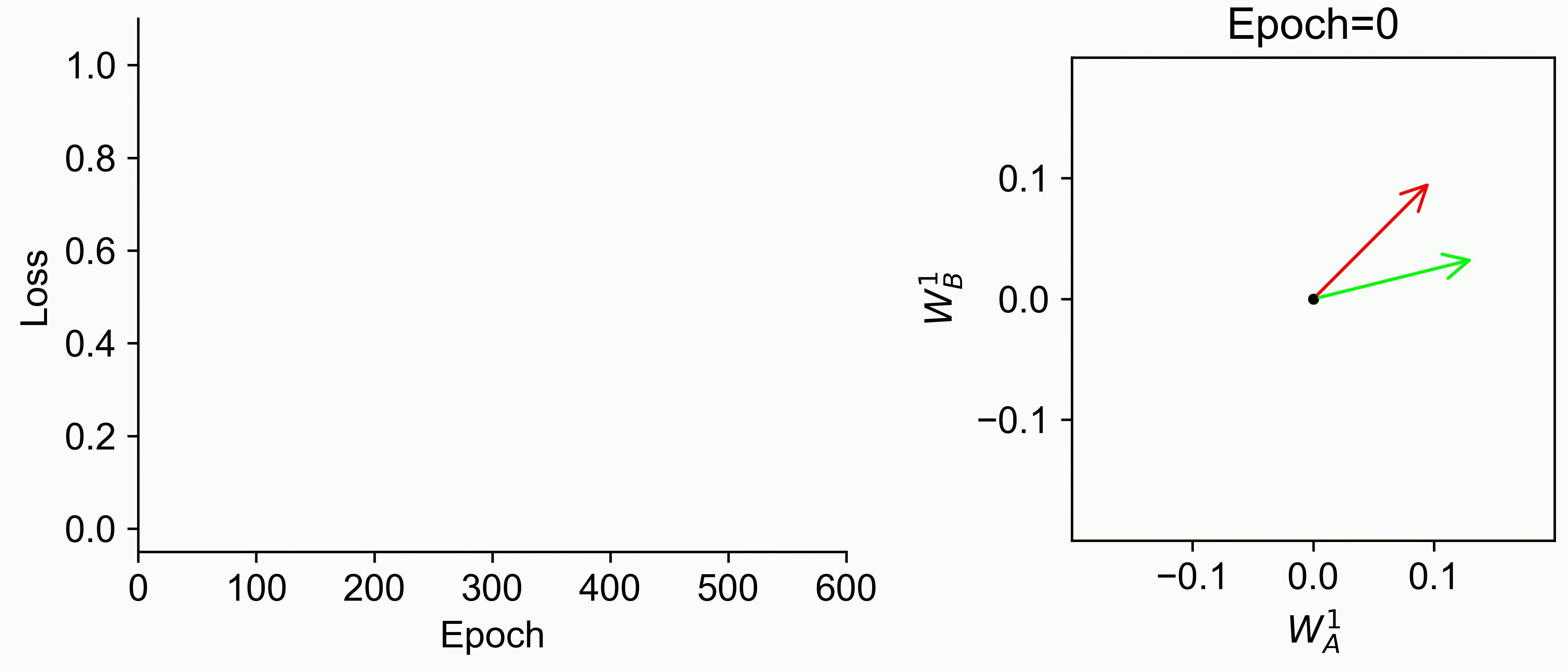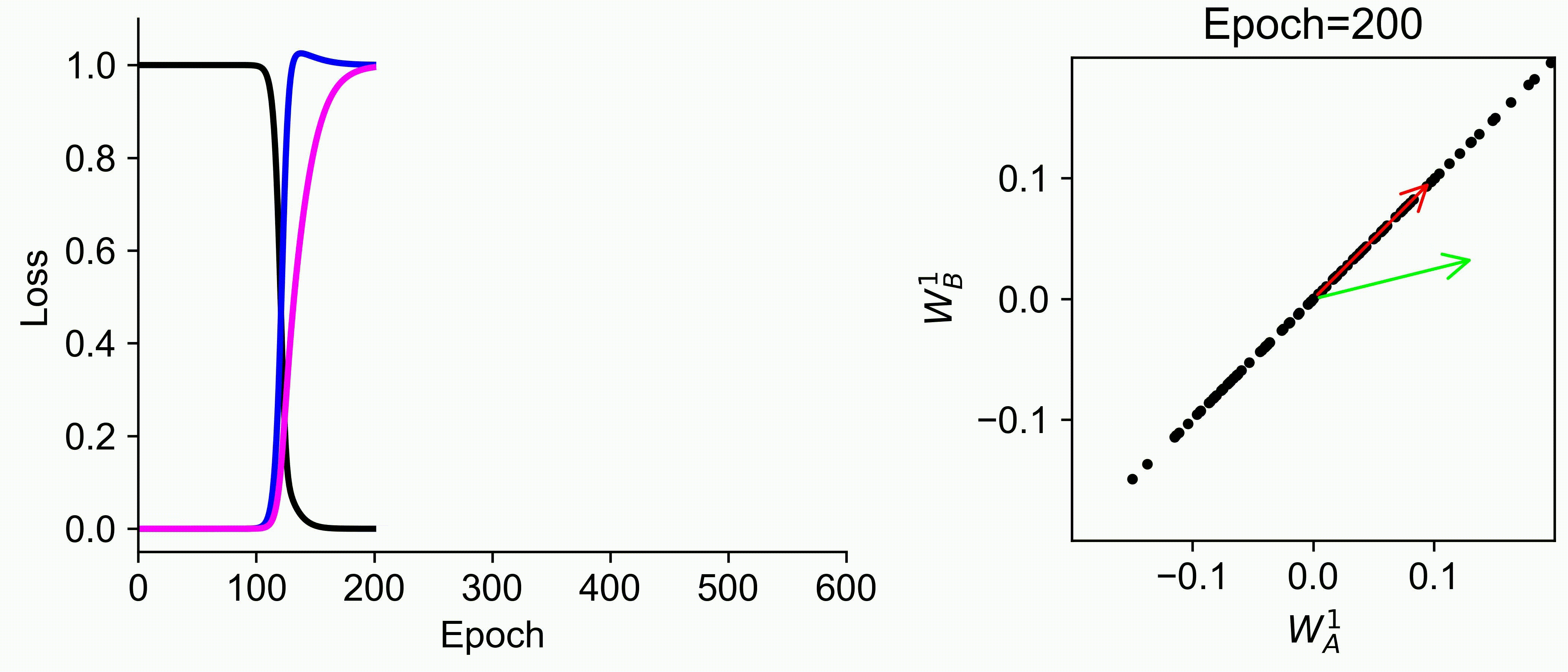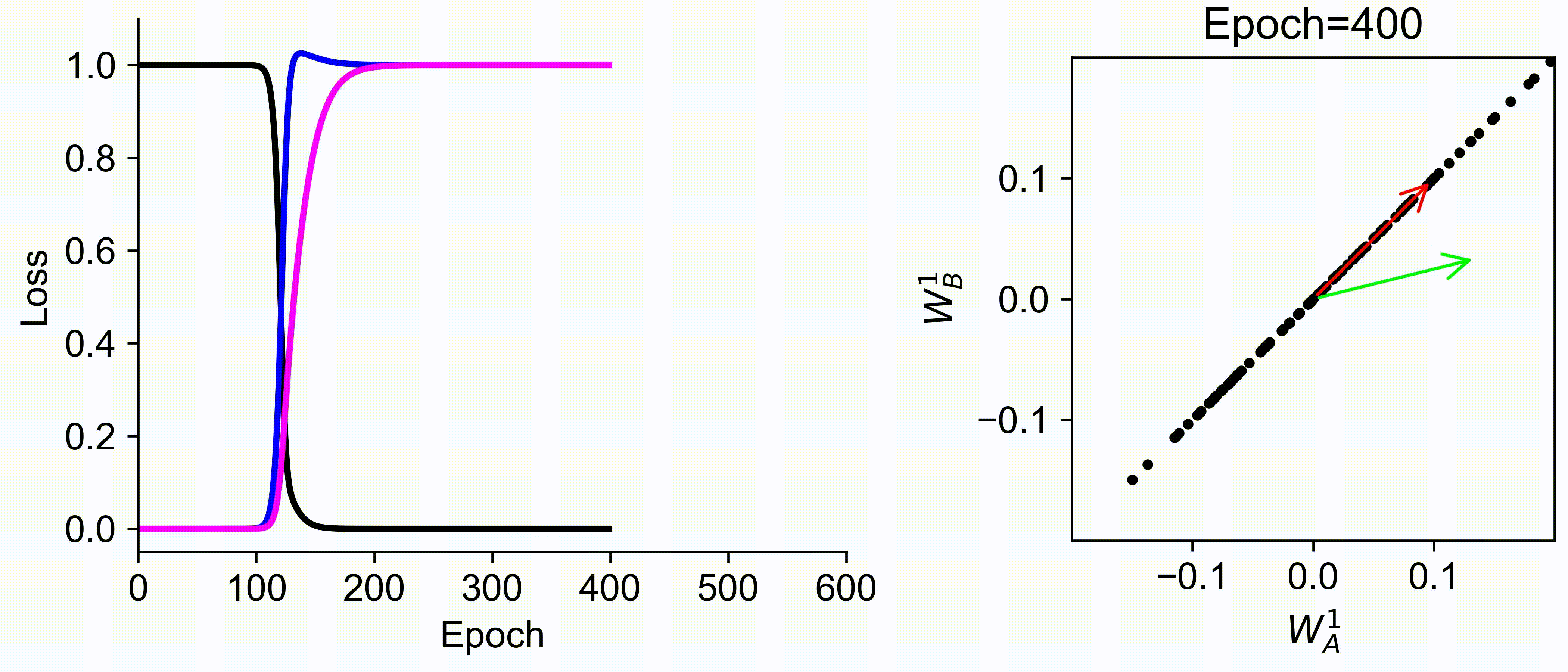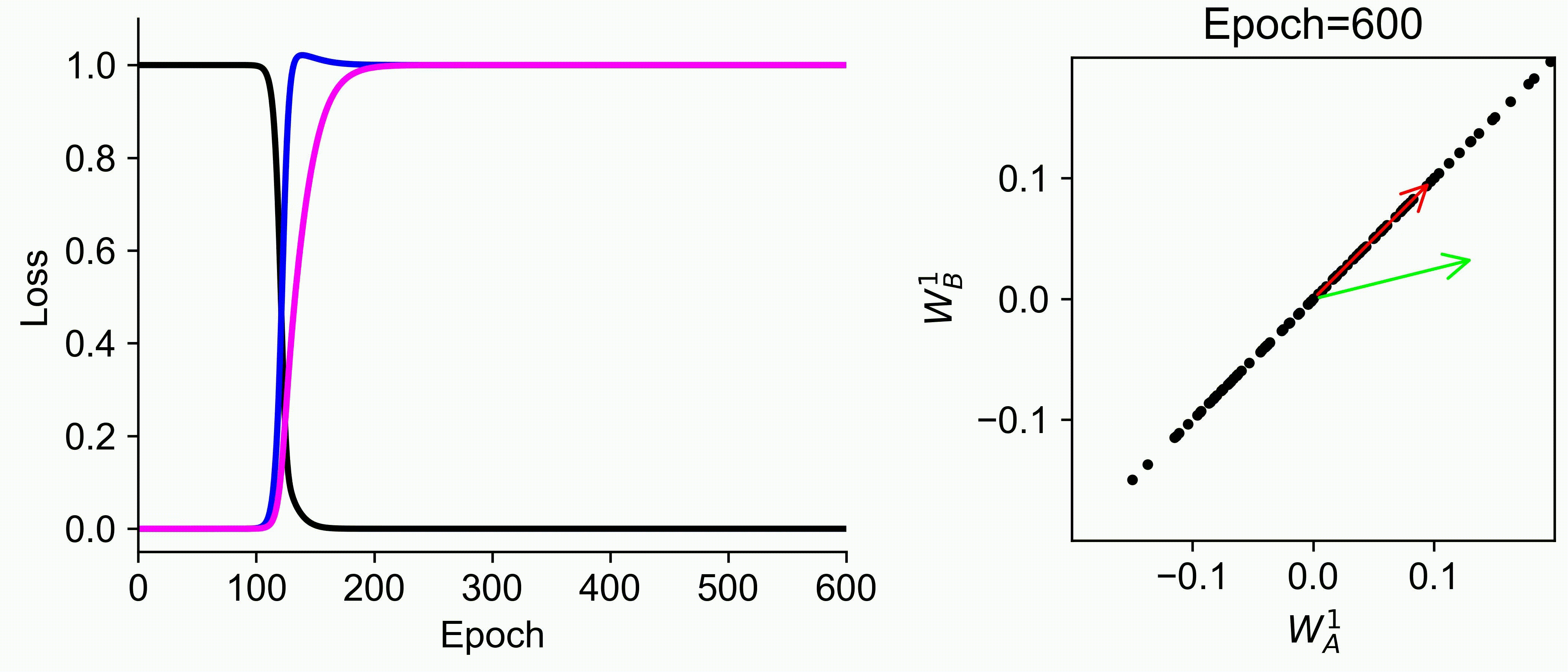
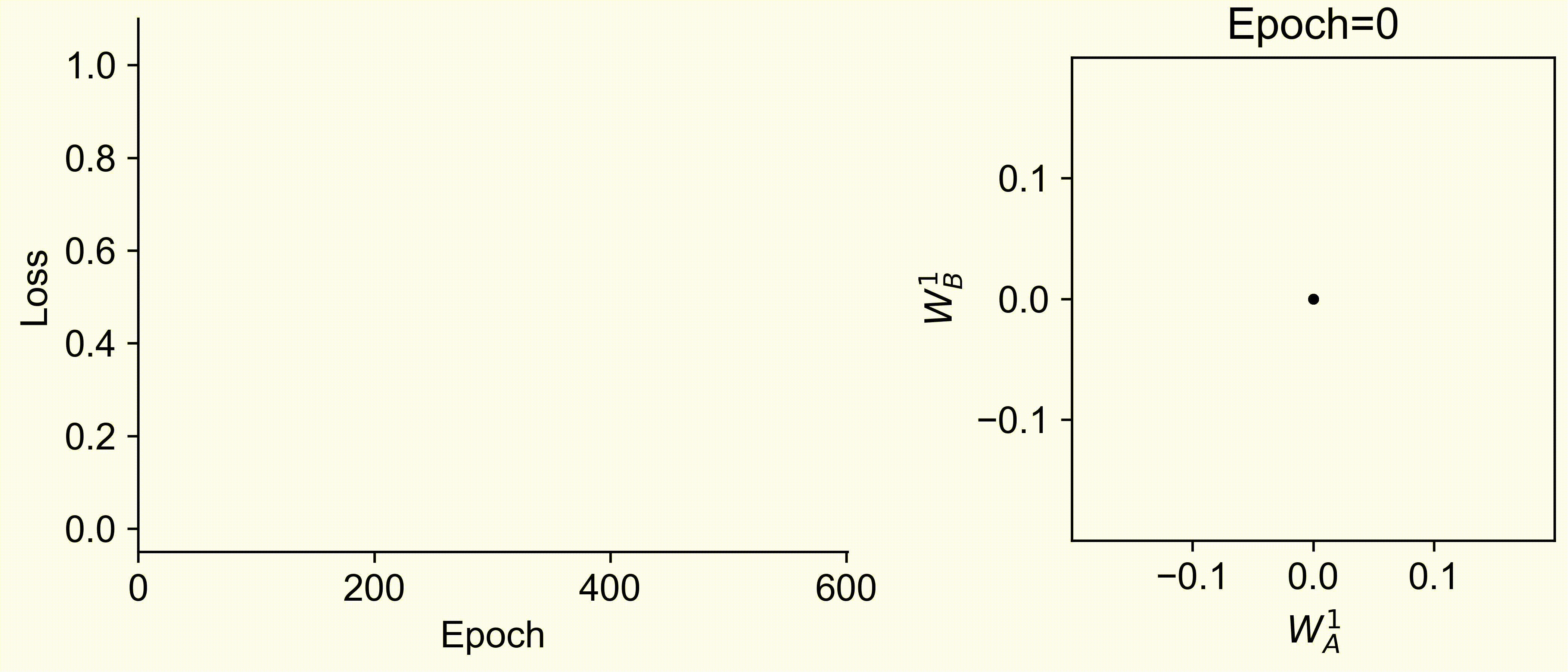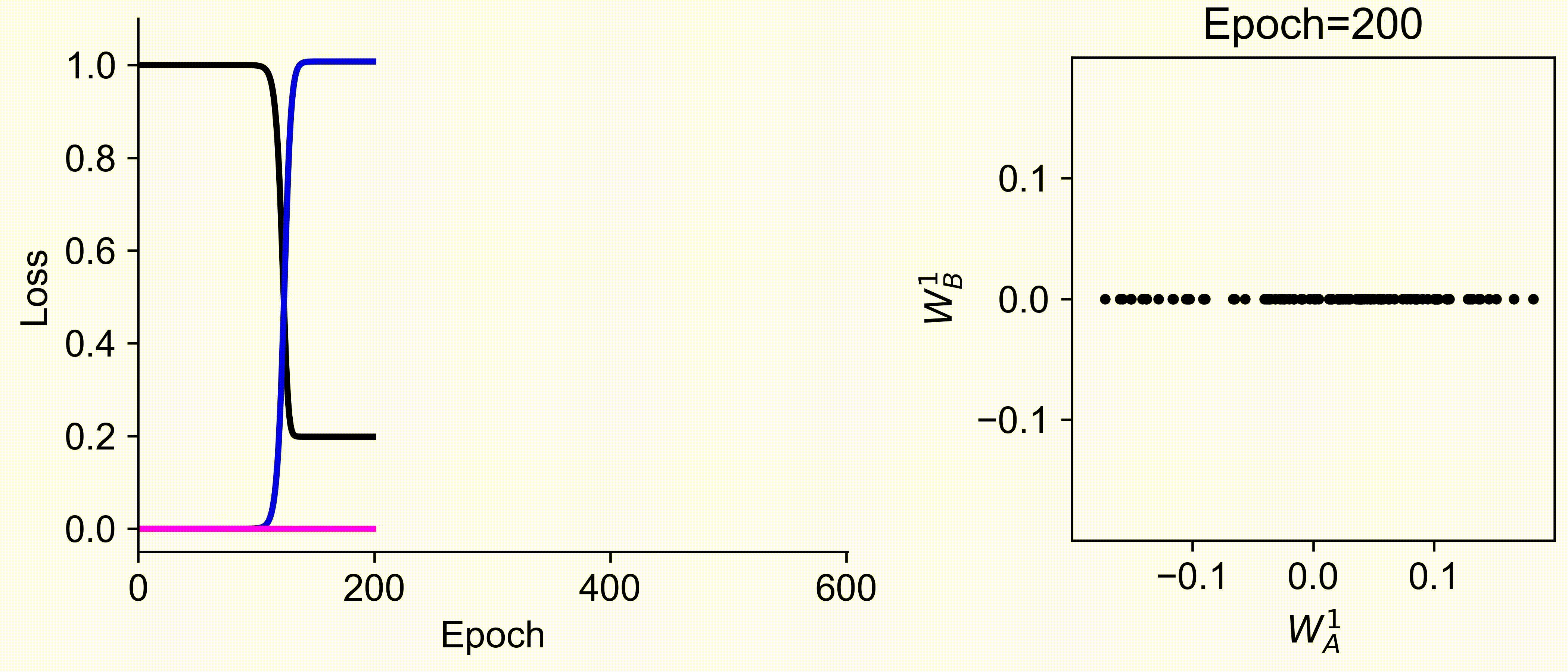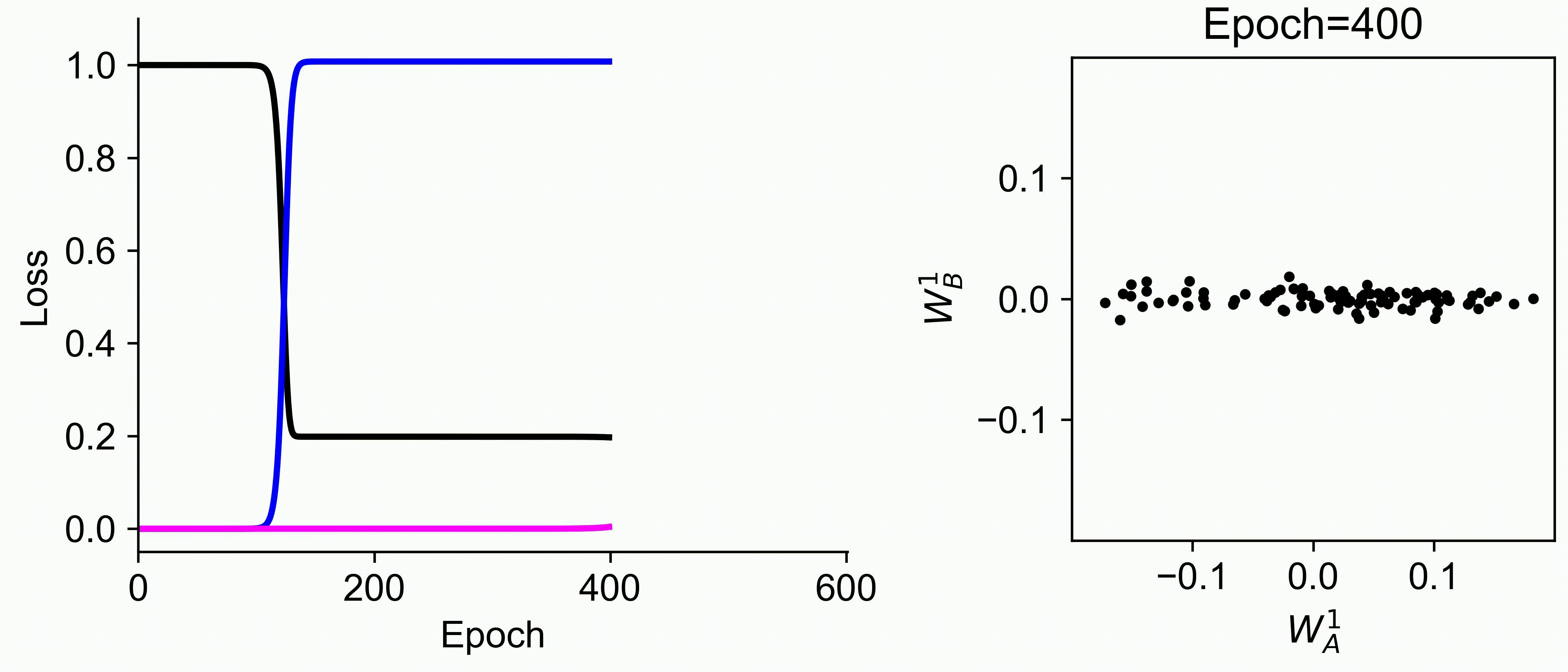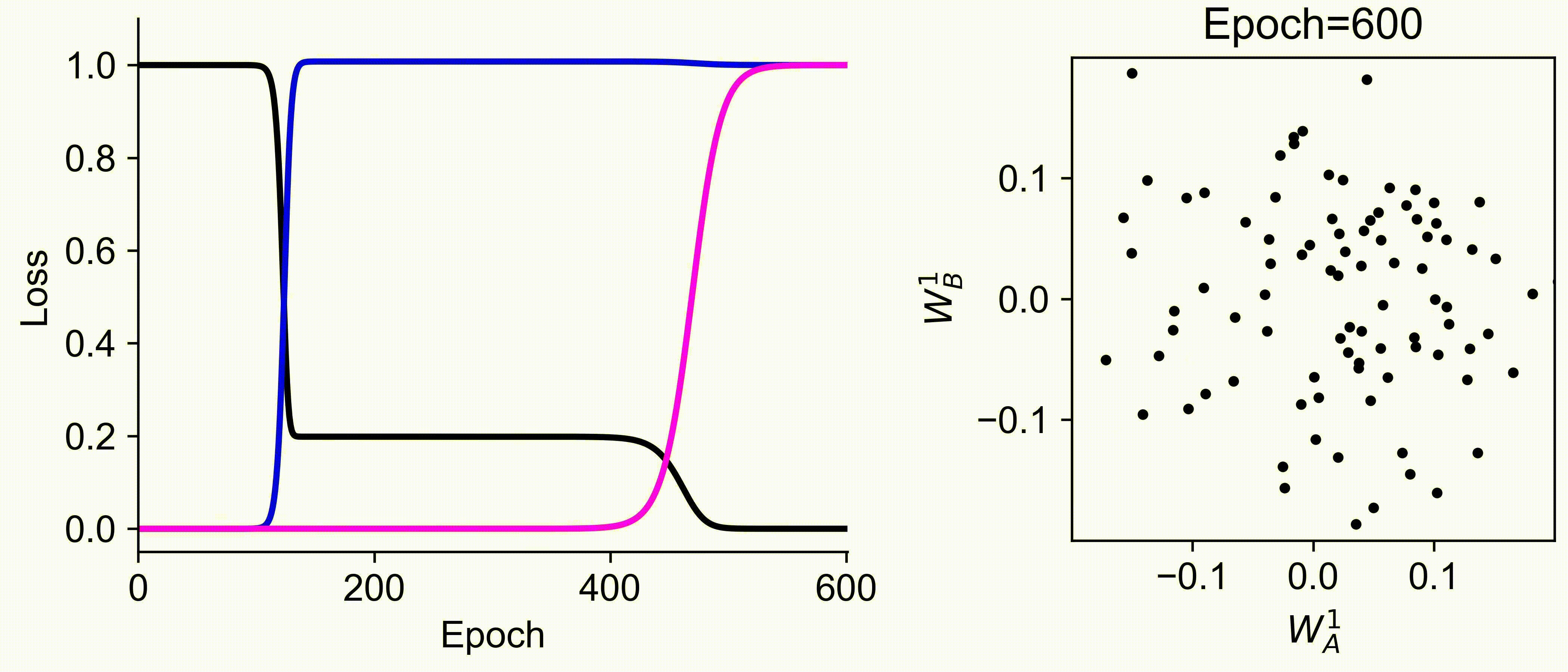
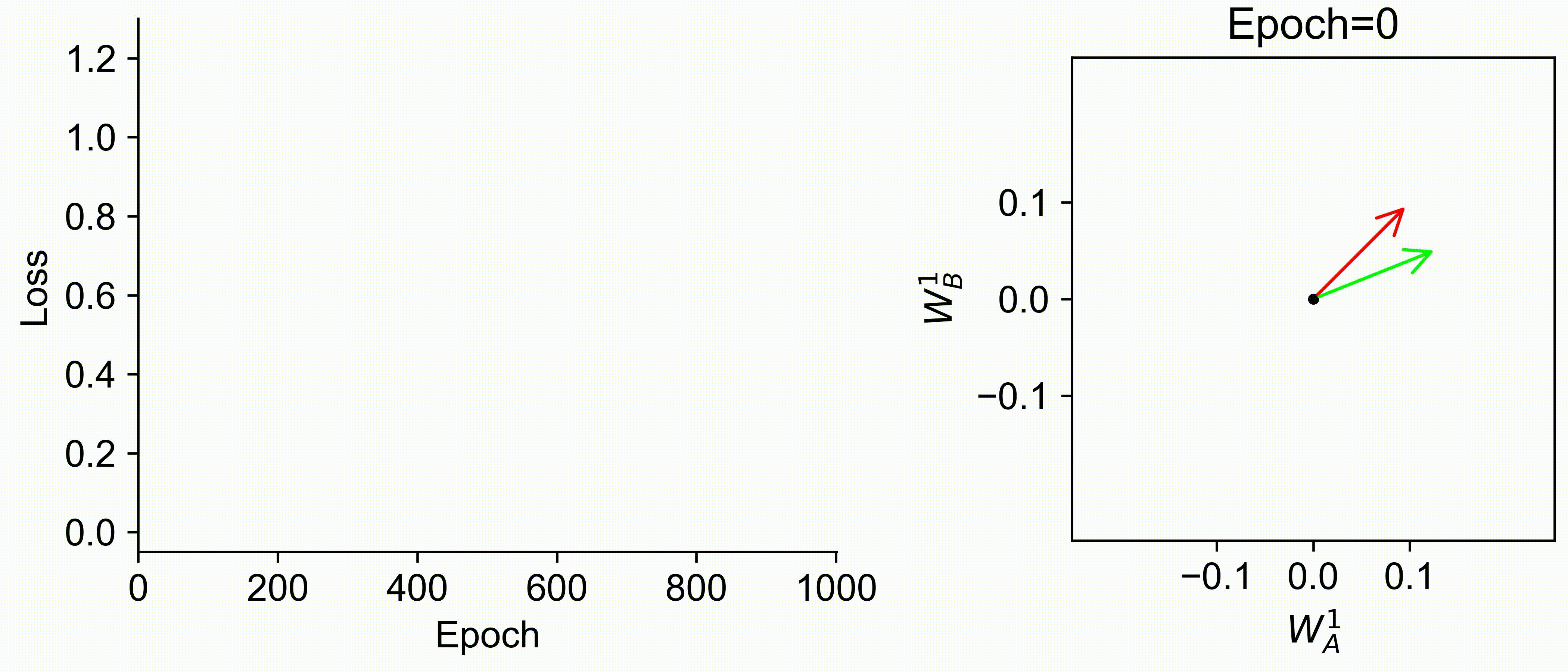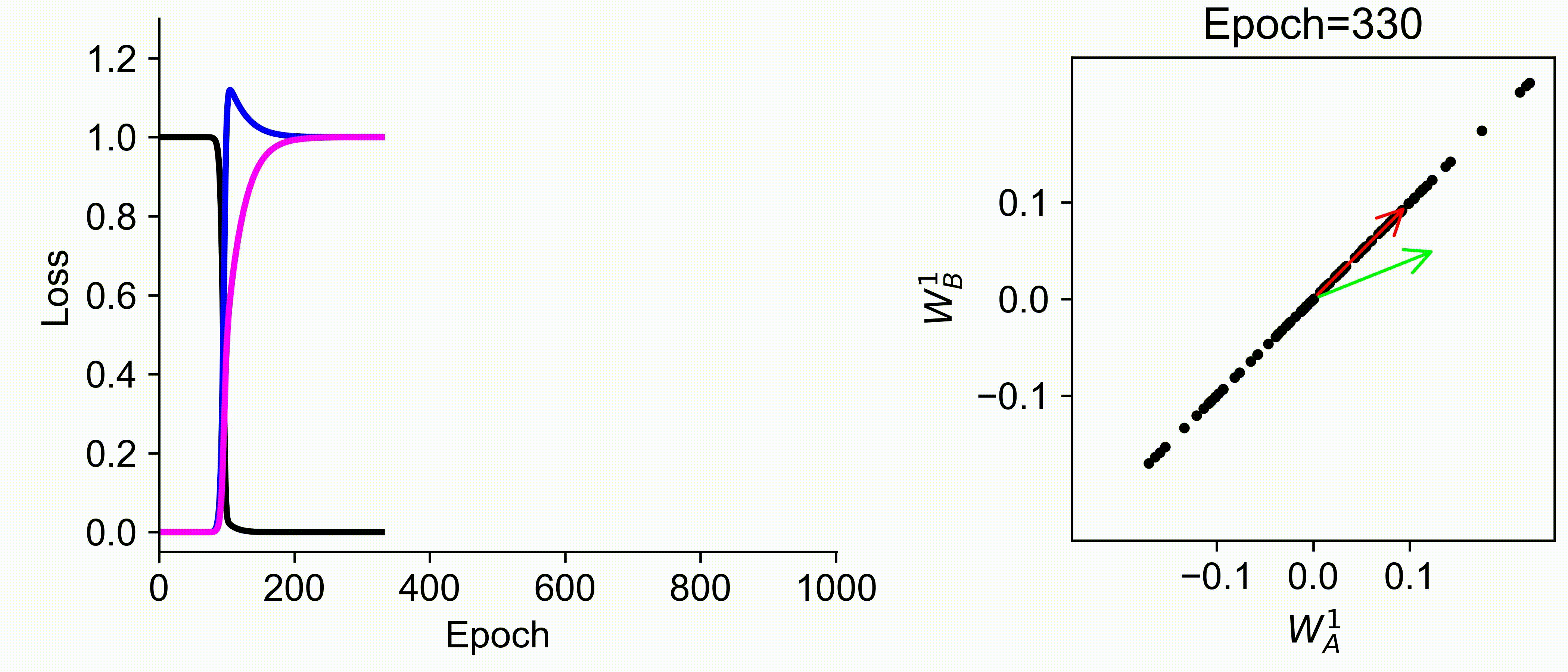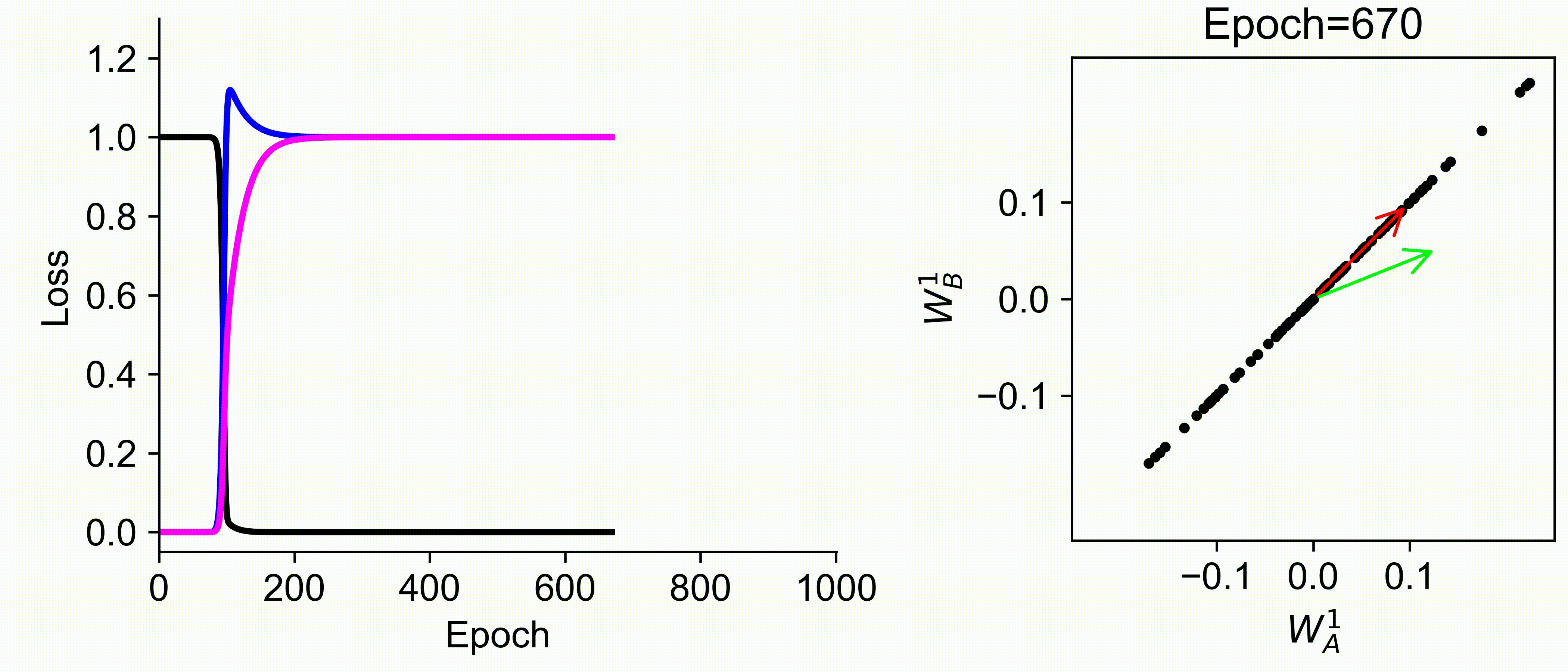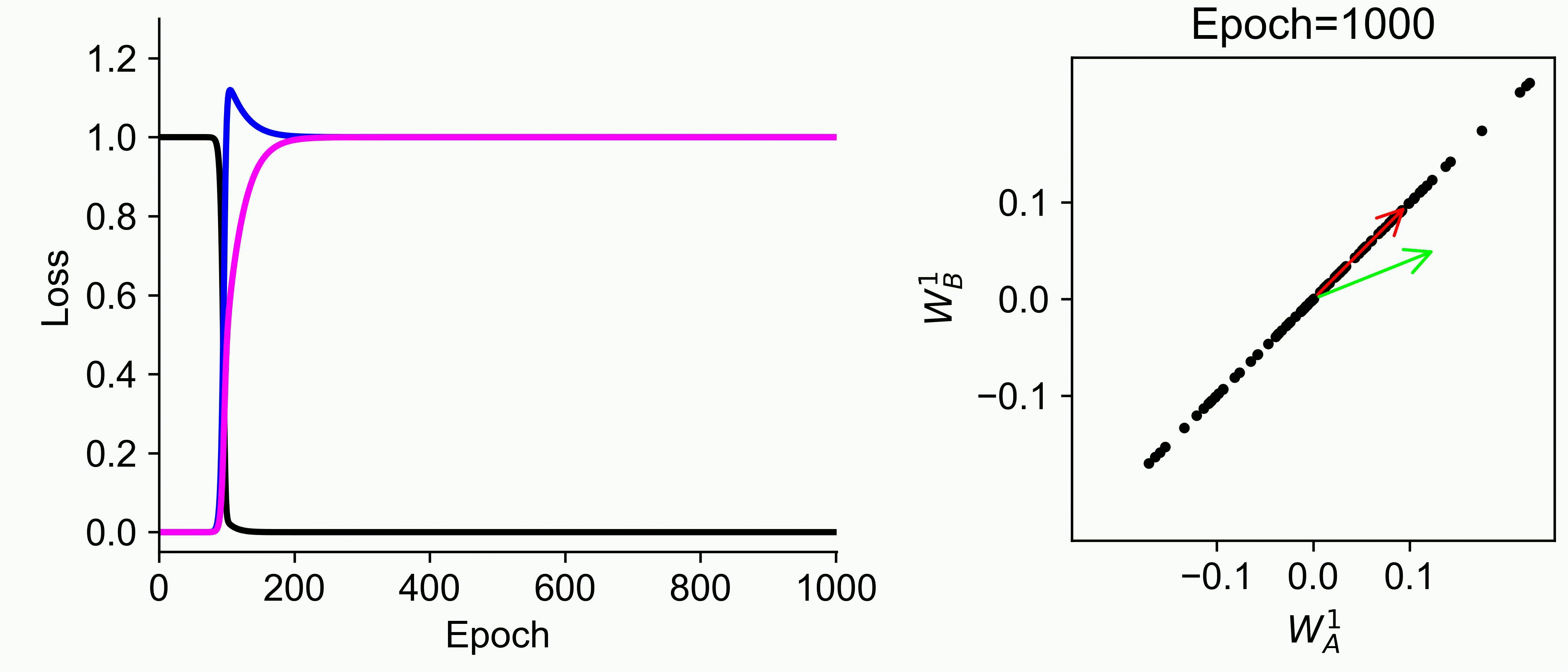
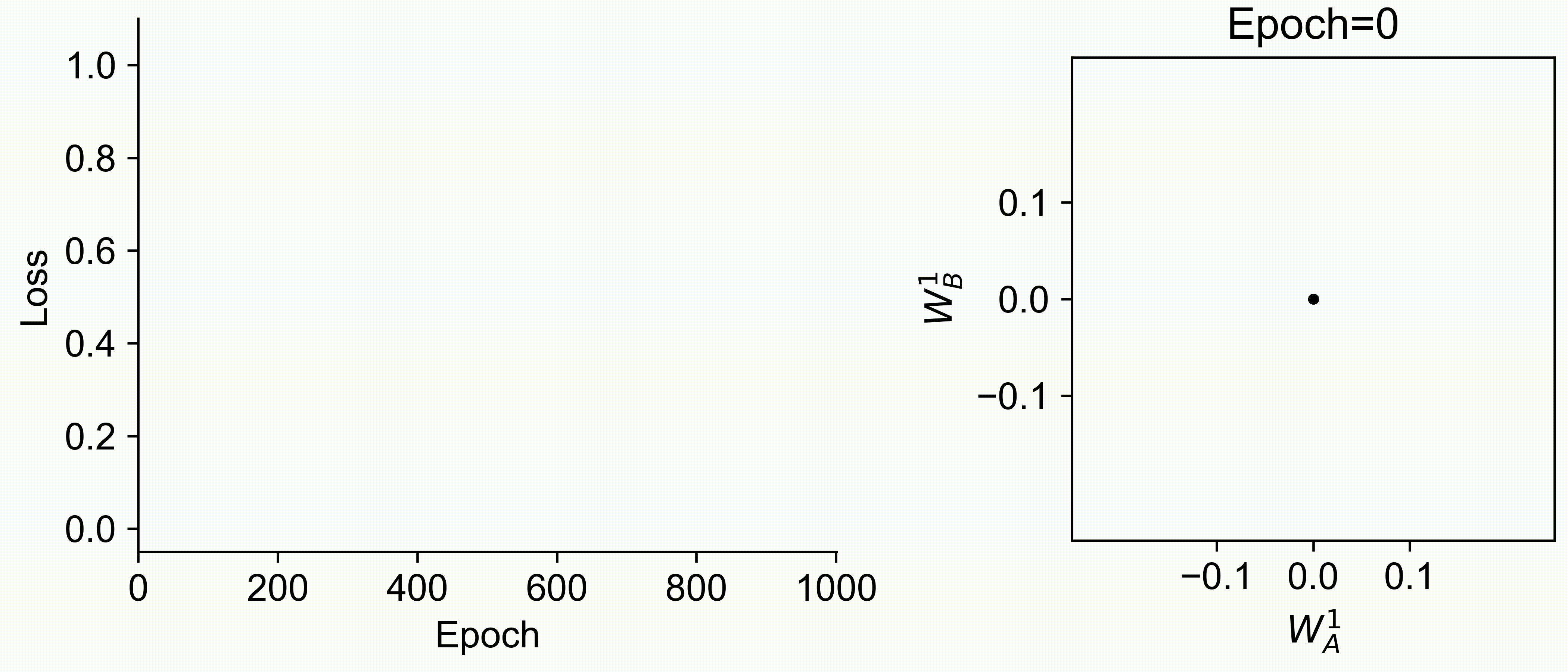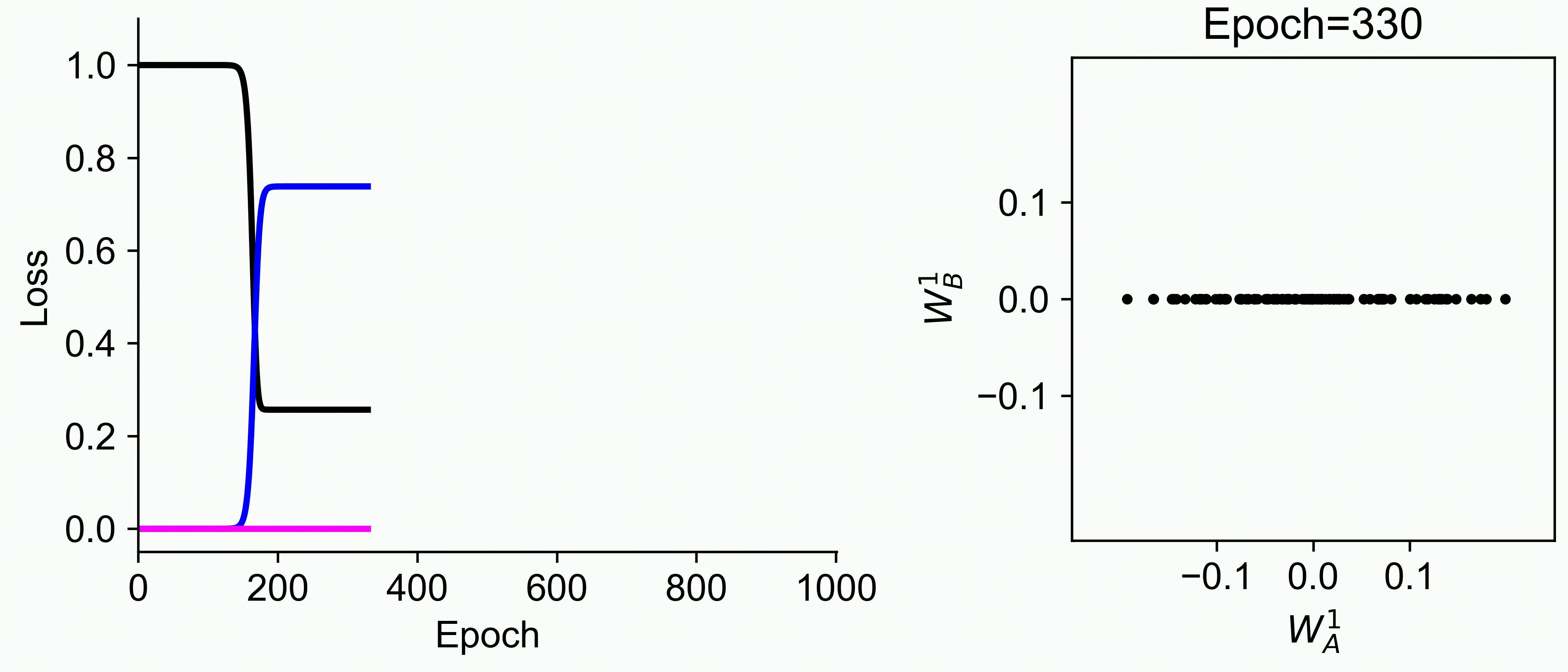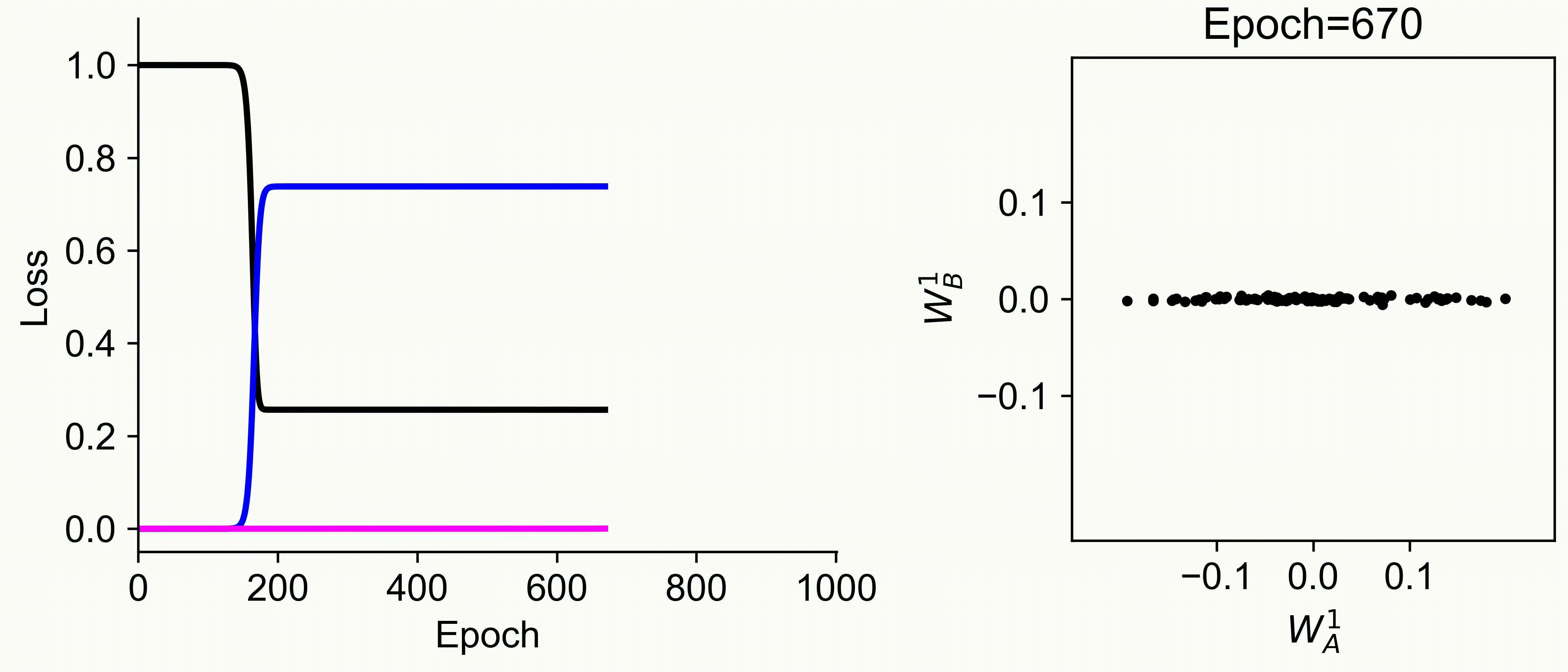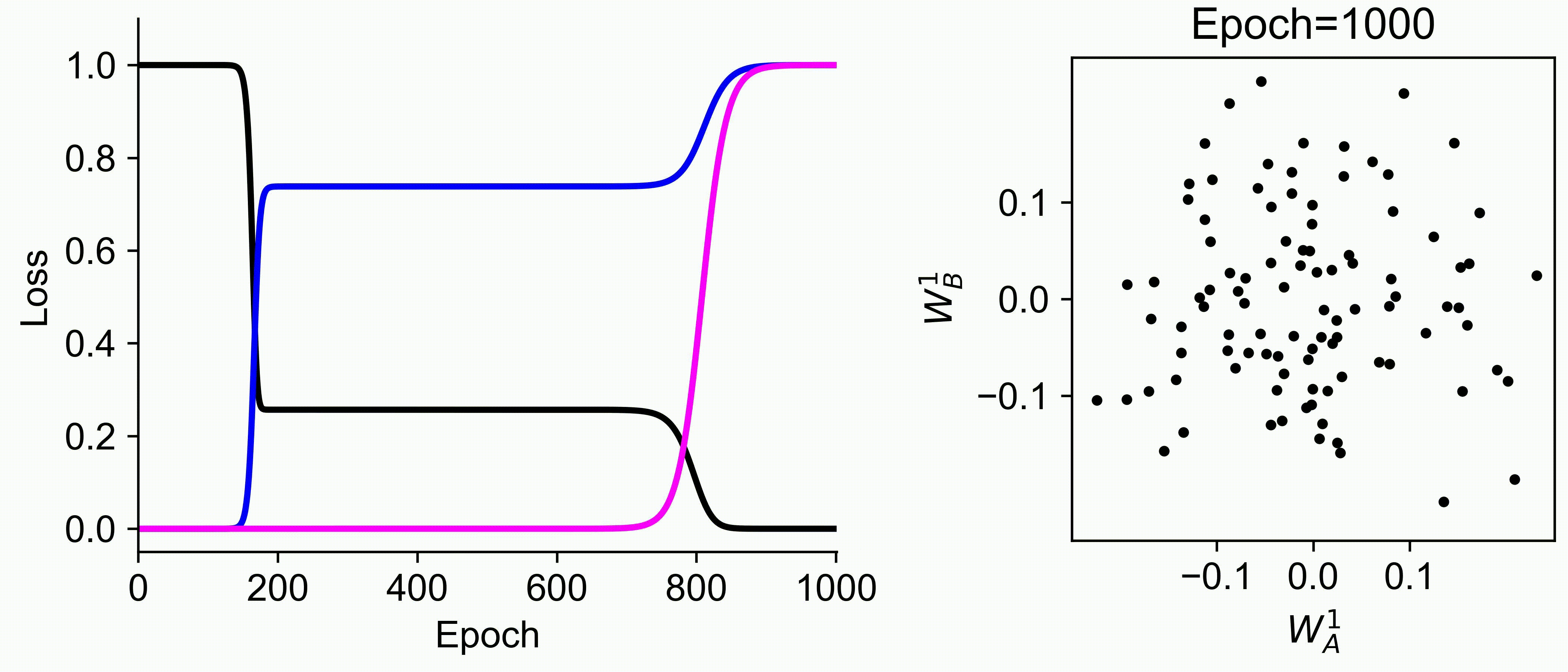
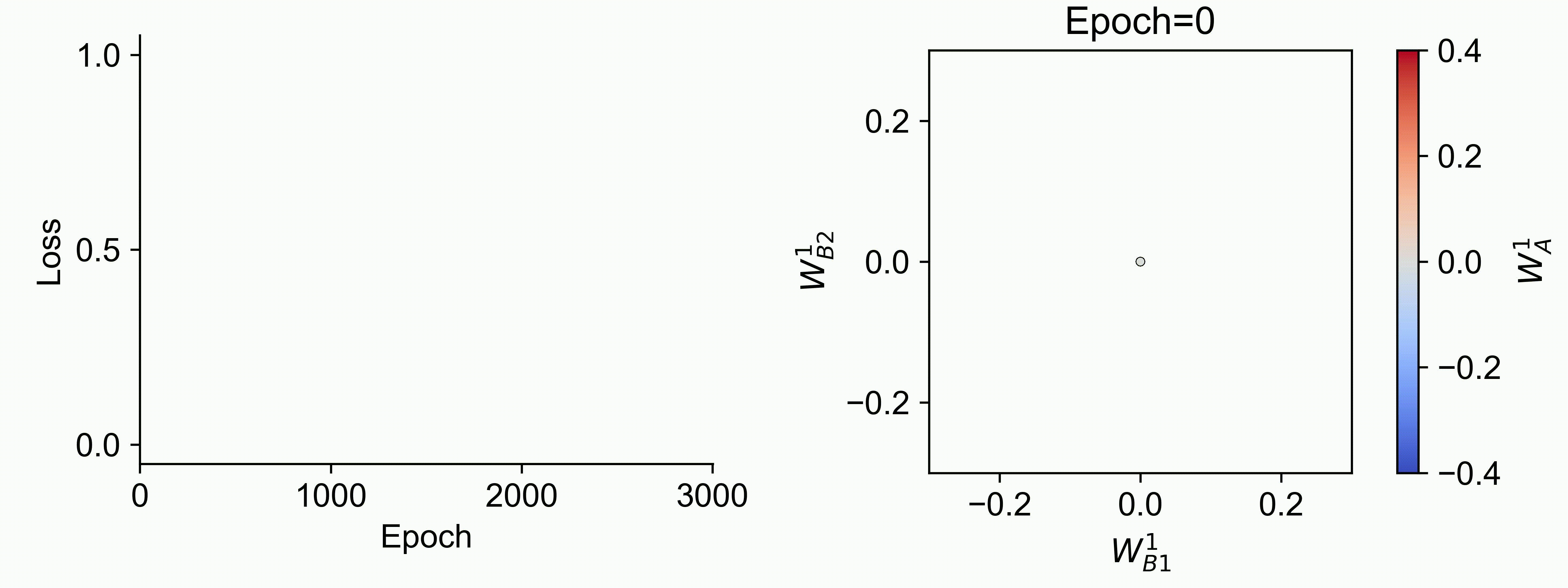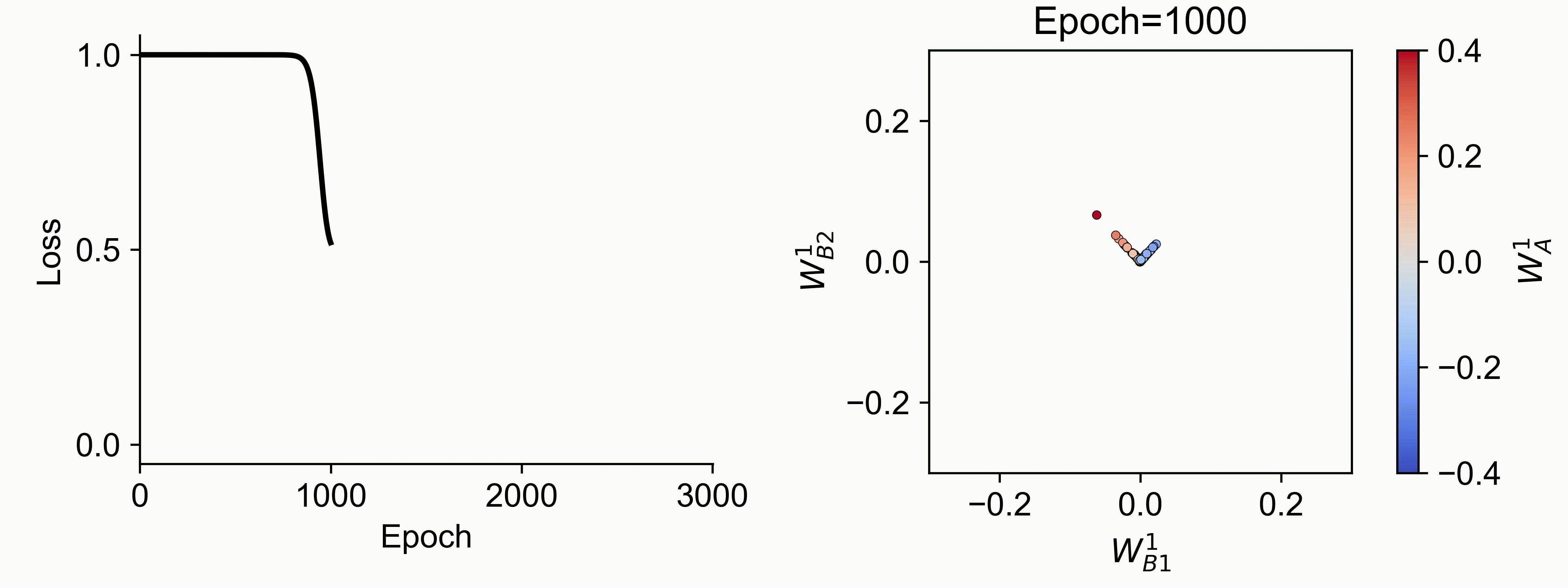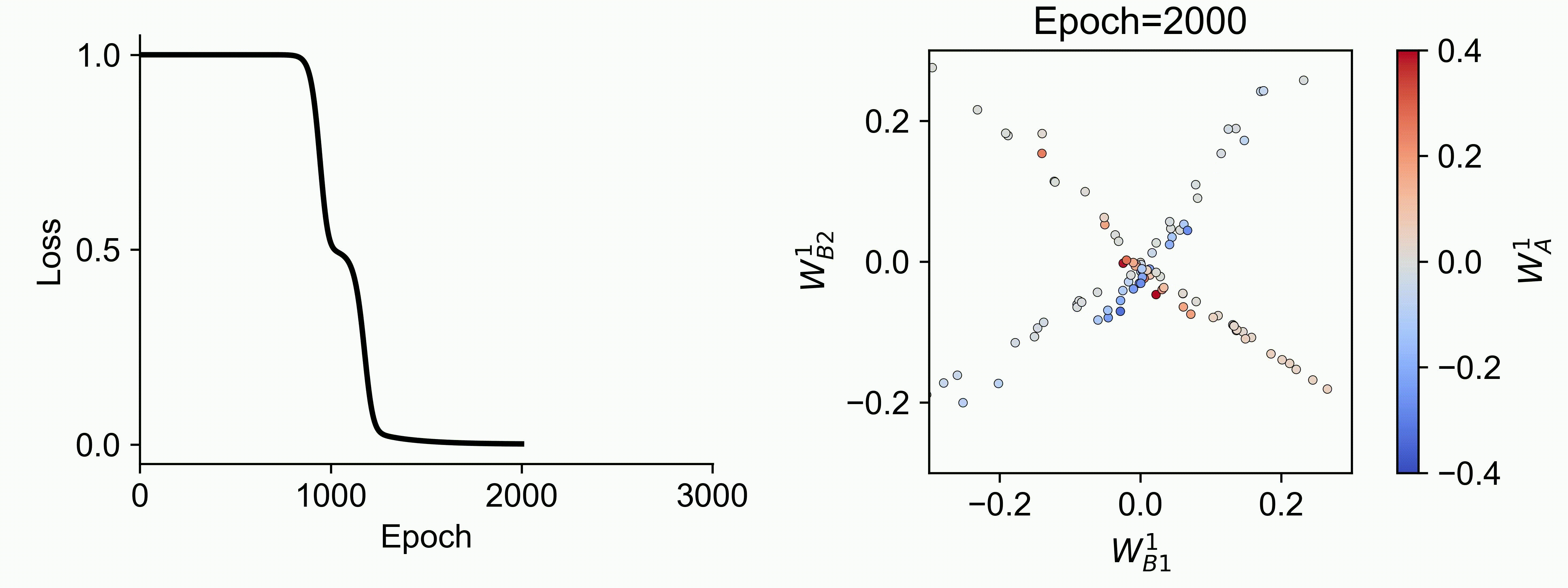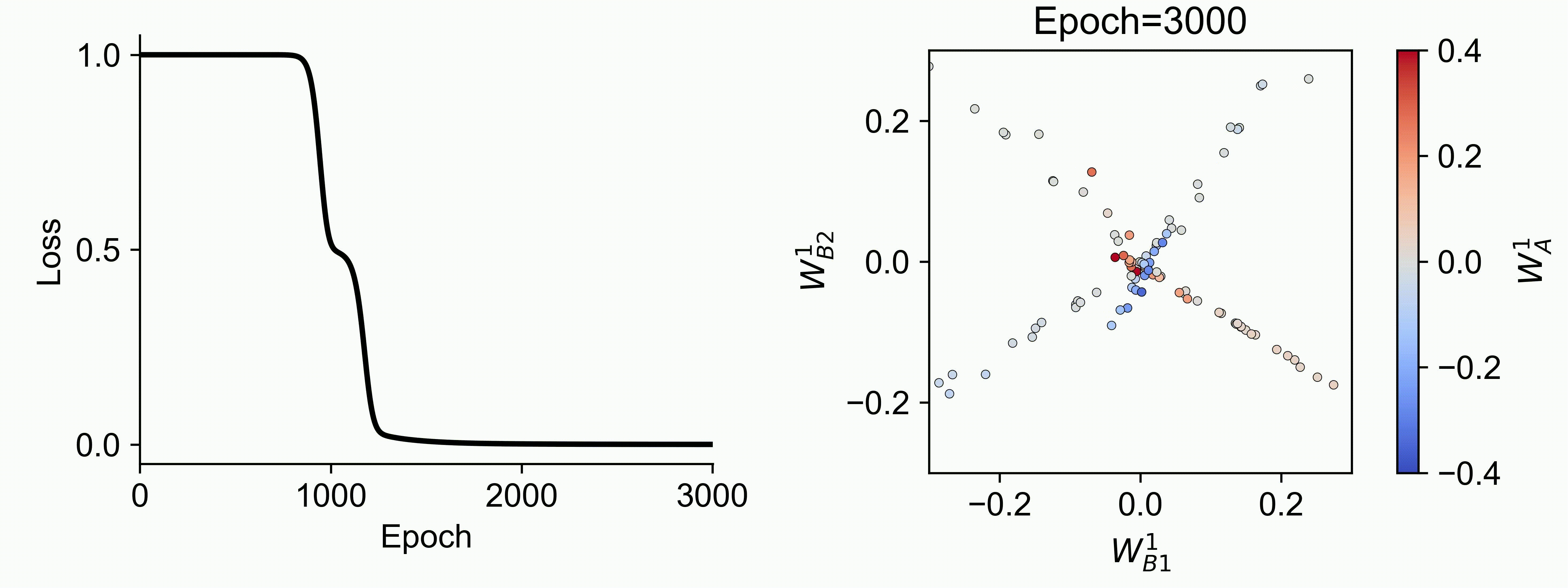
Using multiple input streams simultaneously to train multimodal neural networks is intuitively advantageous but practically challenging. A key challenge is unimodal bias, where a network overly relies on one modality and ignores others during joint training. We develop a theory of unimodal bias with multimodal deep linear networks to understand how architecture and data statistics influence this bias. This is the first work to calculate the duration of the unimodal phase in learning as a function of the depth at which modalities are fused within the network, dataset statistics, and initialization. We show that the deeper the layer at which fusion occurs, the longer the unimodal phase. A long unimodal phase can lead to a generalization deficit and permanent unimodal bias in the overparametrized regime. Our results, derived for multimodal linear networks, extend to nonlinear networks in certain settings. Taken together, this work illuminates pathologies of multimodal learning under joint training, showing that late and intermediate fusion architectures can give rise to long unimodal phases and permanent unimodal bias.

Loss and weights trajectories of early fusion (upper row) and late fusion (lower row) linear networks.

---

Supplementary Material

Effect of positive/negative correlations between modalities

	Early fusion linear network		Late fusion linear network
Positive correlation
Negative correlation

Nonlinear network and heterogeneous task

We present a simple heterogeneous task: y=x_A + XOR(x_B) where x_A is a scalar and x_B∈{[1,1], [1,-1],[-1,1], [-1,-1]}. XOR(x_B) refers to performing XOR to the two dimensions of x_B. We plot the loss and weights trajectories for different variances of x_A.

	Early fusion ReLU network		Late fusion ReLU network
σA=1
σA=2
σA=3

We observe that two-layer late fusion ReLU networks always learn this task successfully, forming the four perpendicular XOR features. However, two-layer early fusion ReLU networks do not learn consistent XOR features and can even fail to learn this task. In the failed cases, the variance of x_A is large so that the network can be stuck at a local minimum where the network only exploits the linear modality. For this heterogeneous task, late fusion networks are advantageous in terms of extracting heterogeneous features from each input modality.

---

This webpage template is borrowed from here.