Saddle-to-Saddle Dynamics Explains A Simplicity Bias
Across Neural Network Architectures 2025 preprint

Yedi Zhang1	Andrew Saxe1,2	Peter Latham1

¹Gatsby Unit, UCL   ²SWC, UCL

---

Abstract

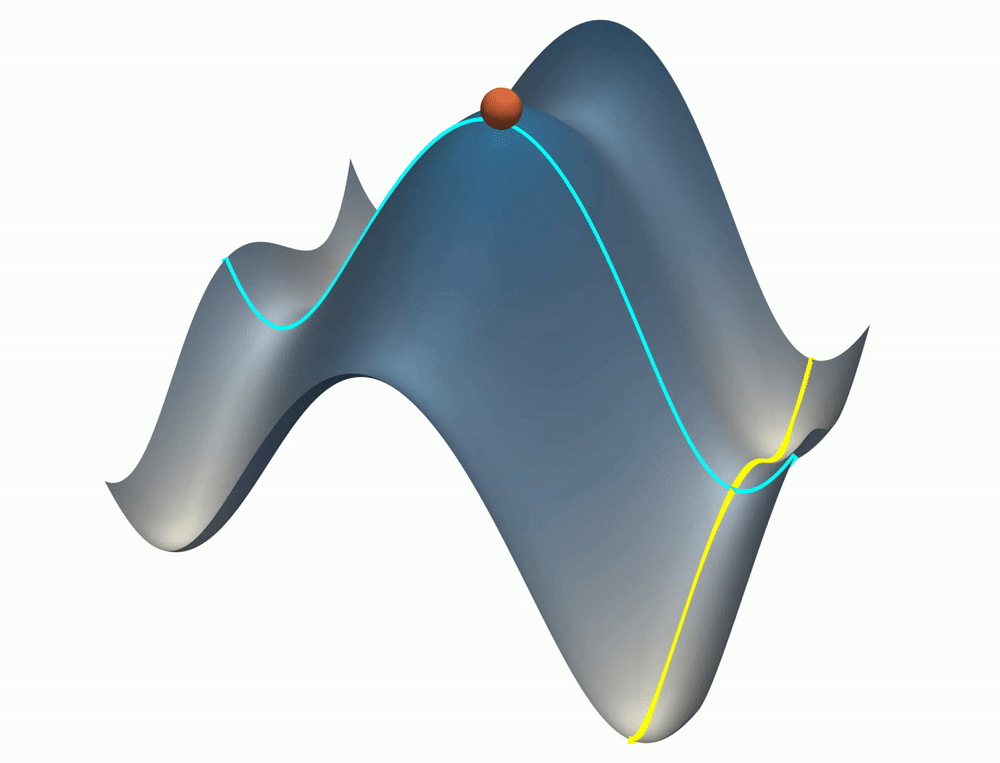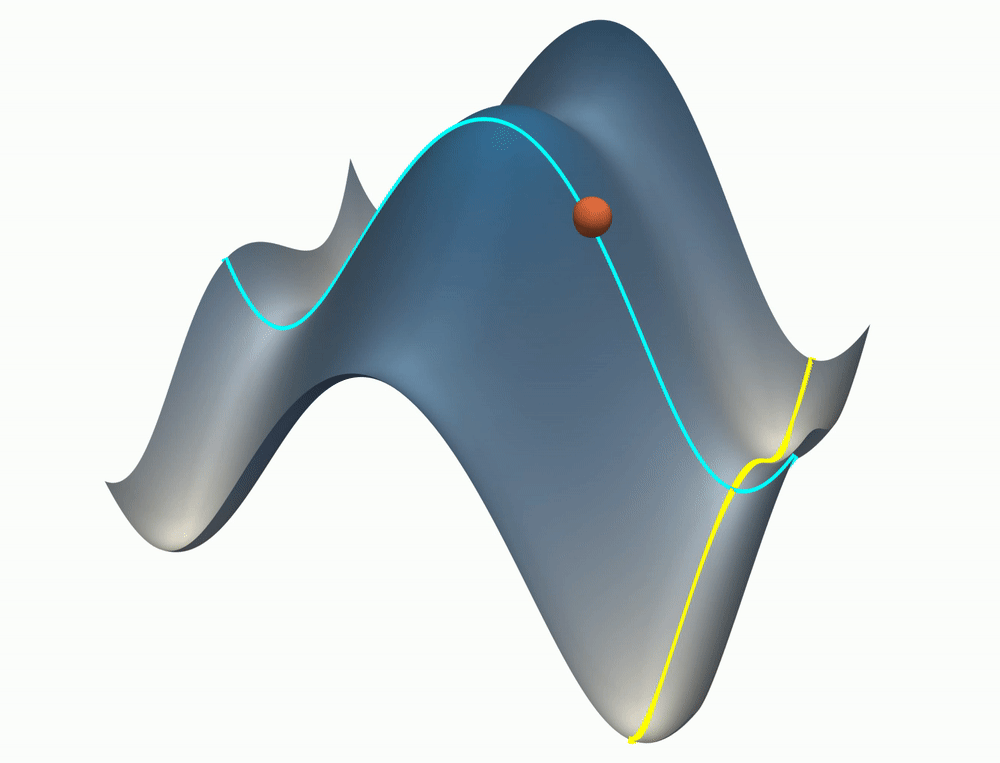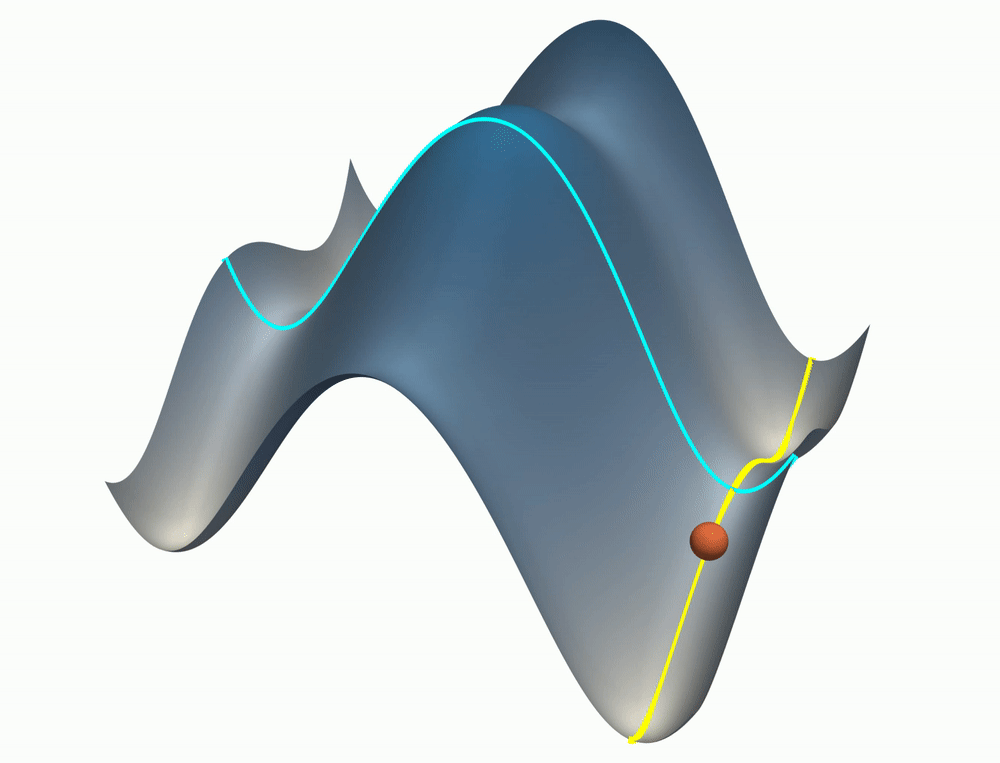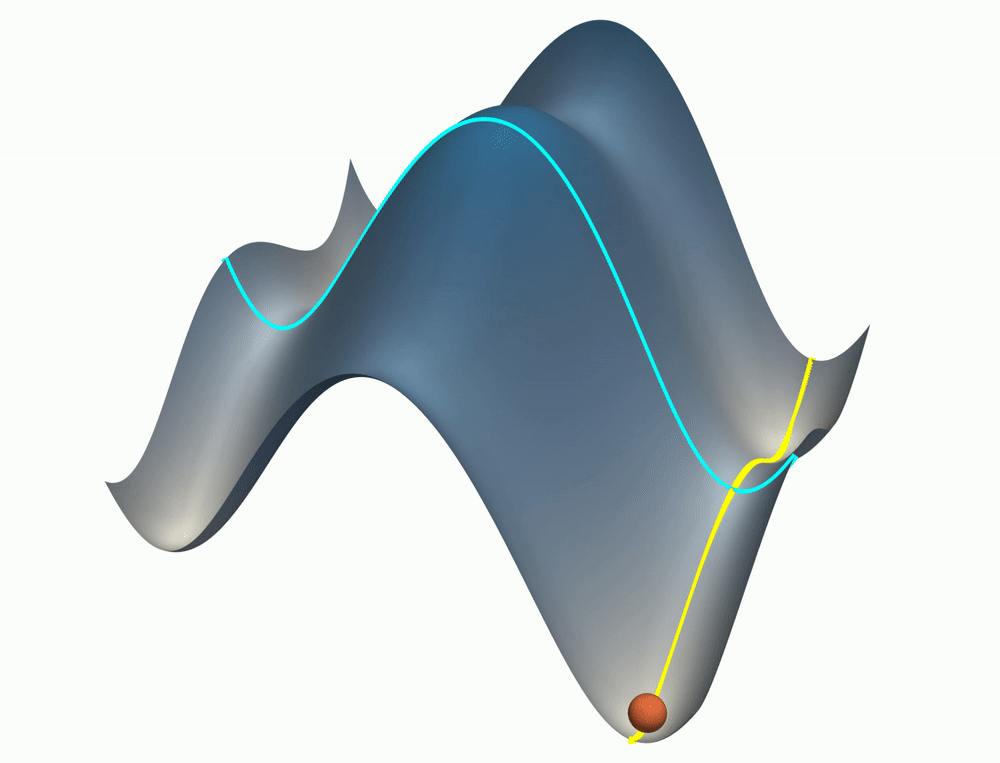
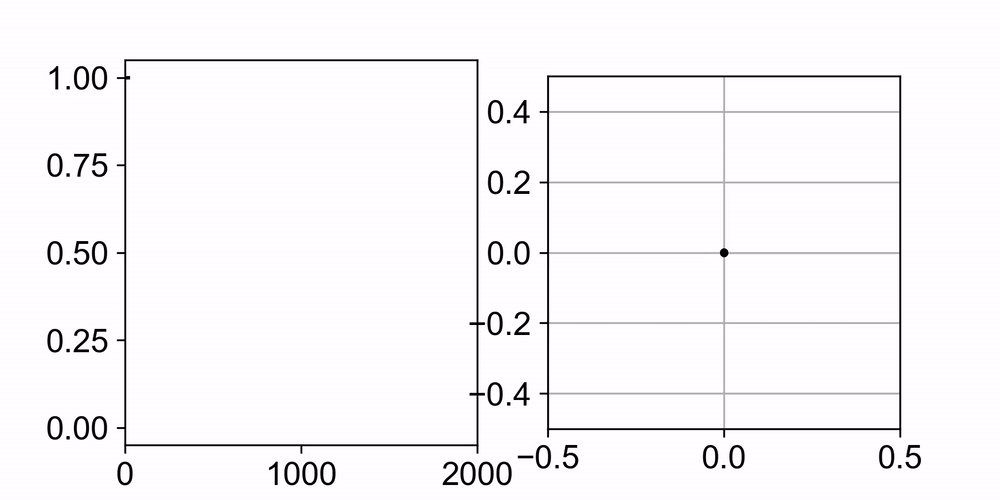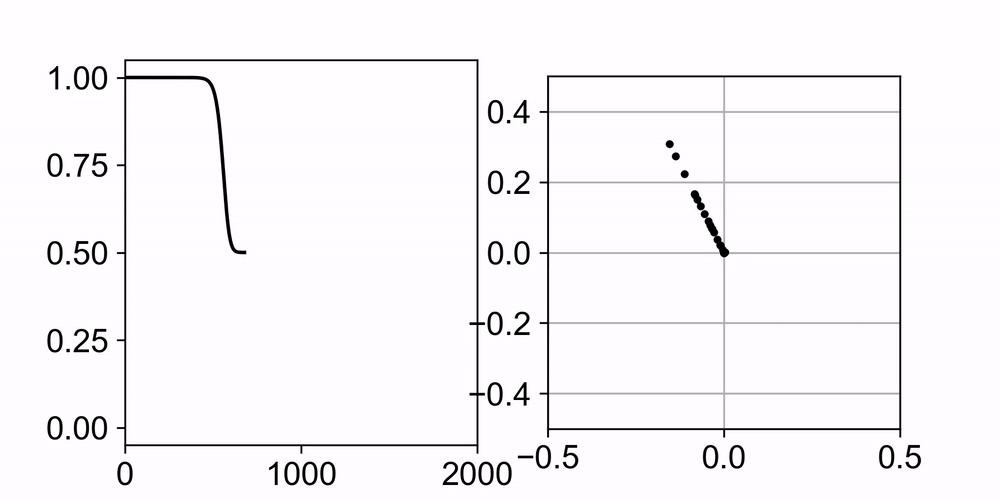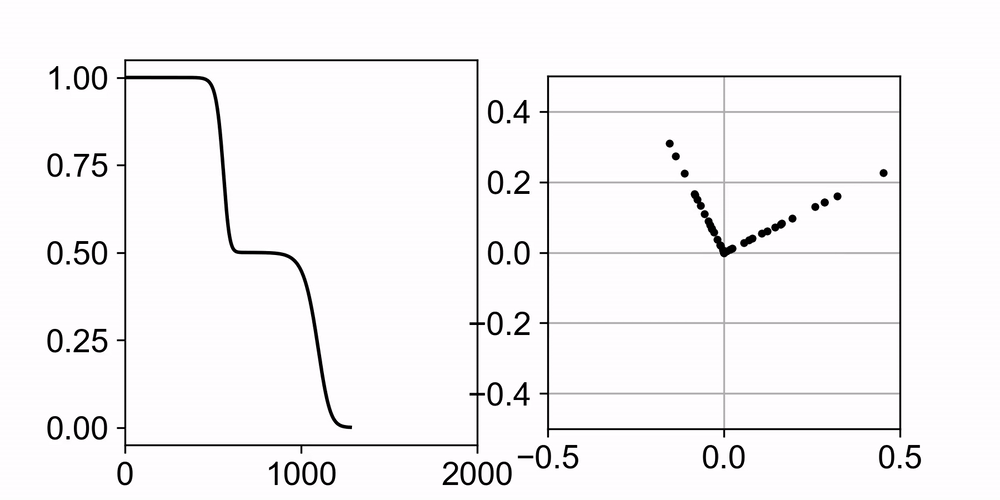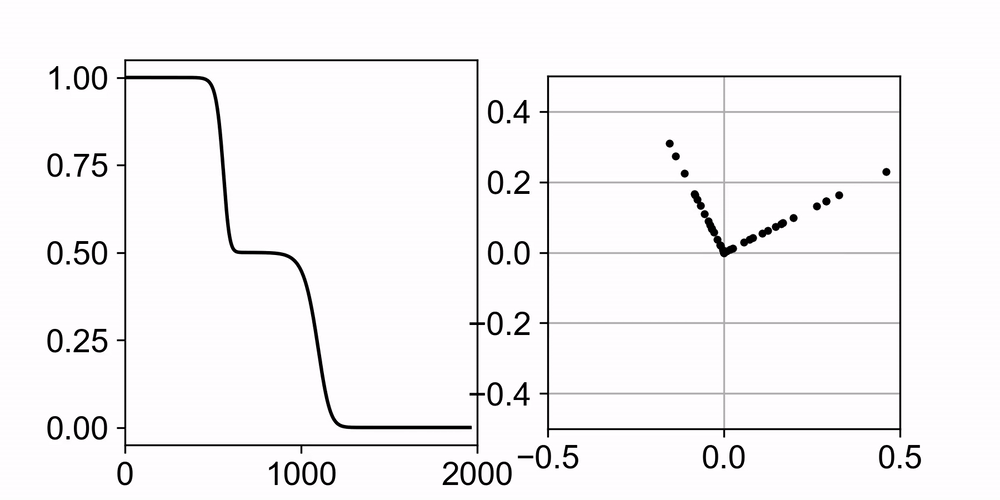
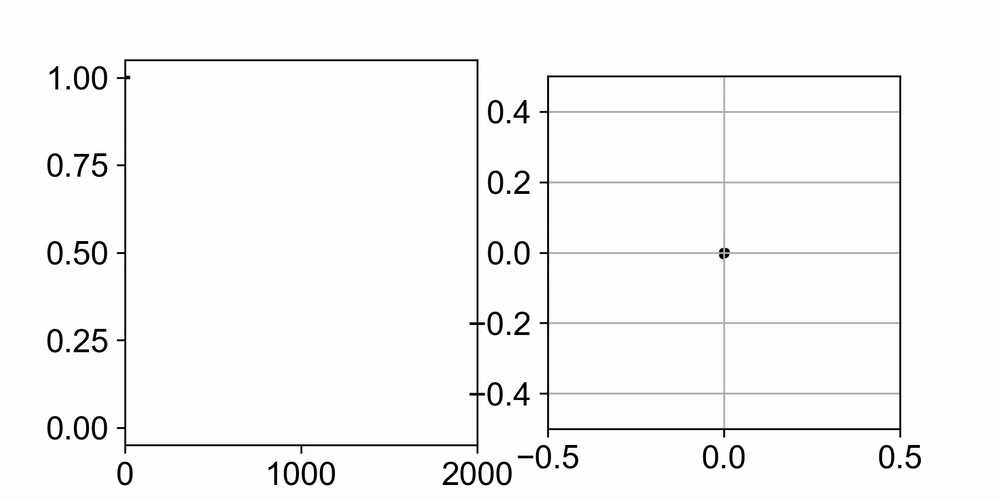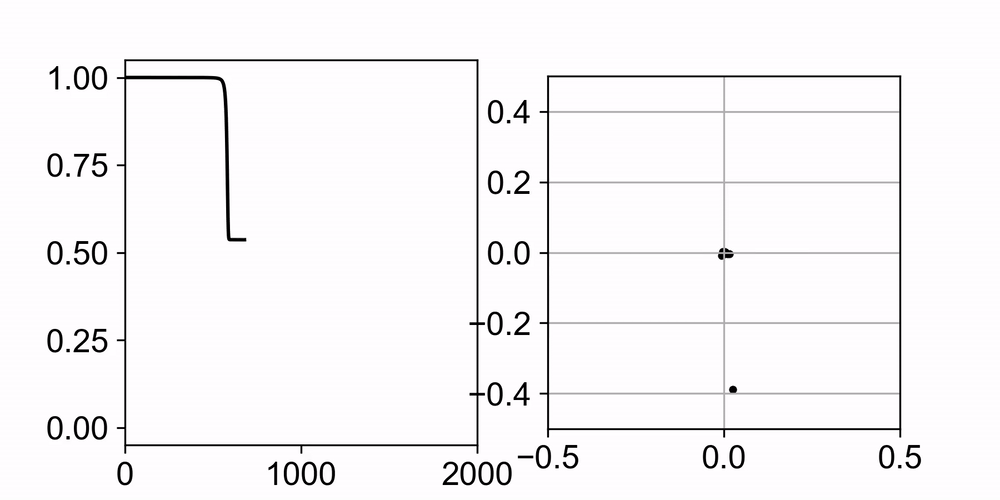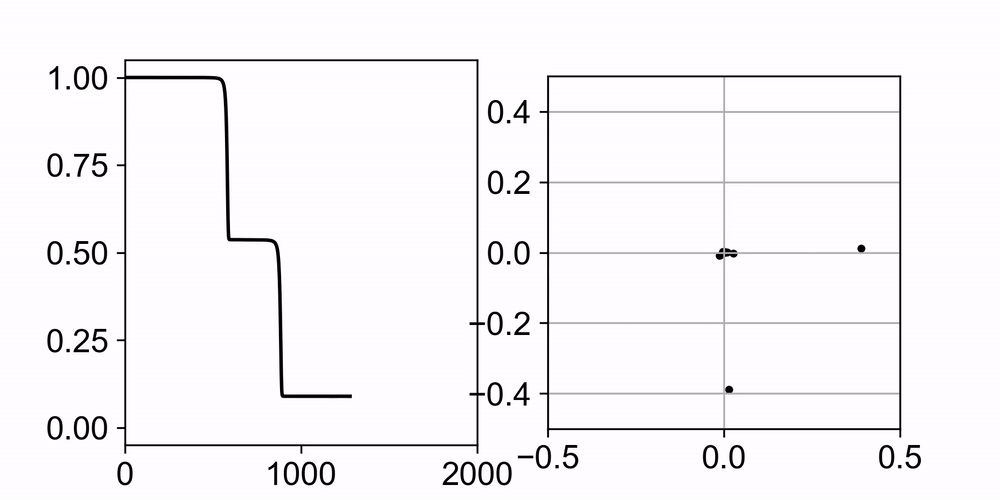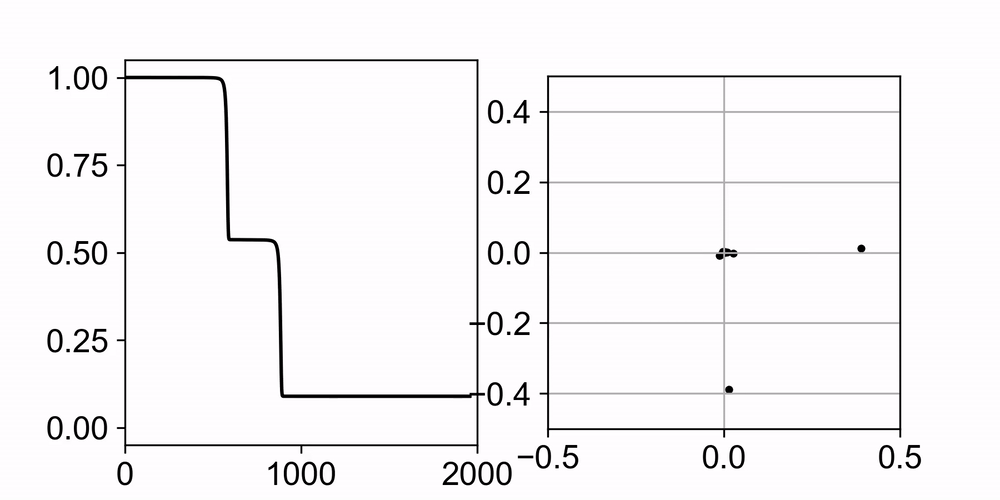
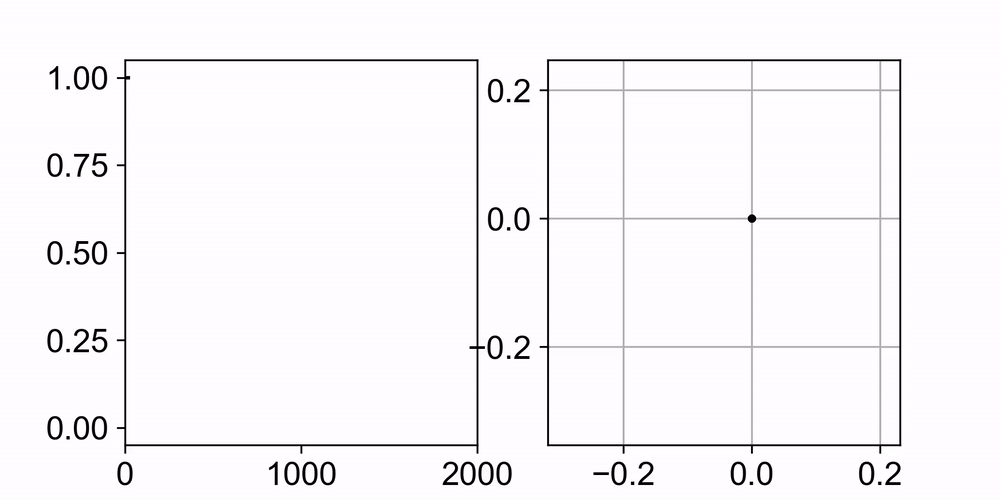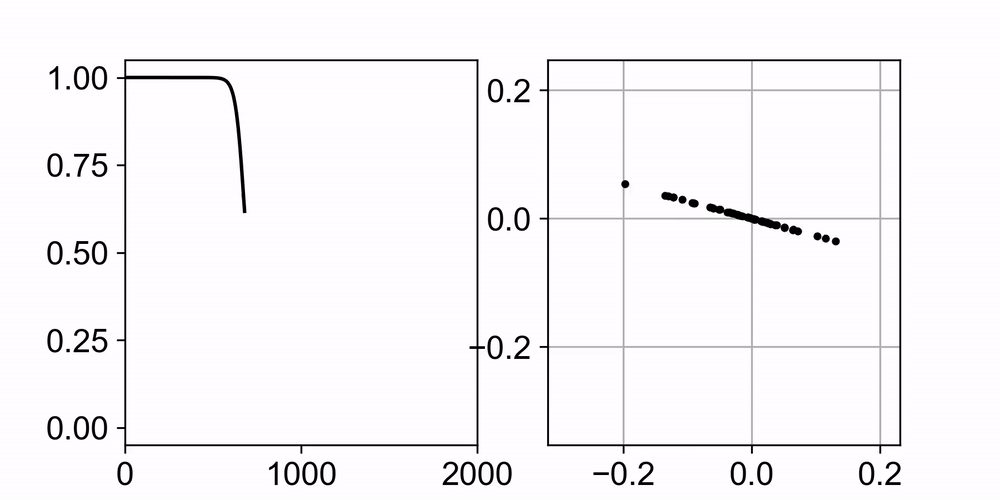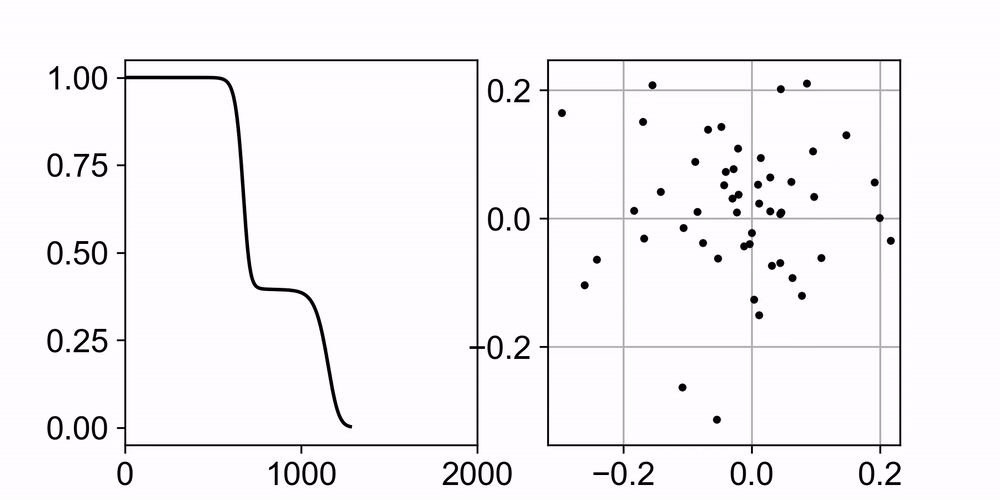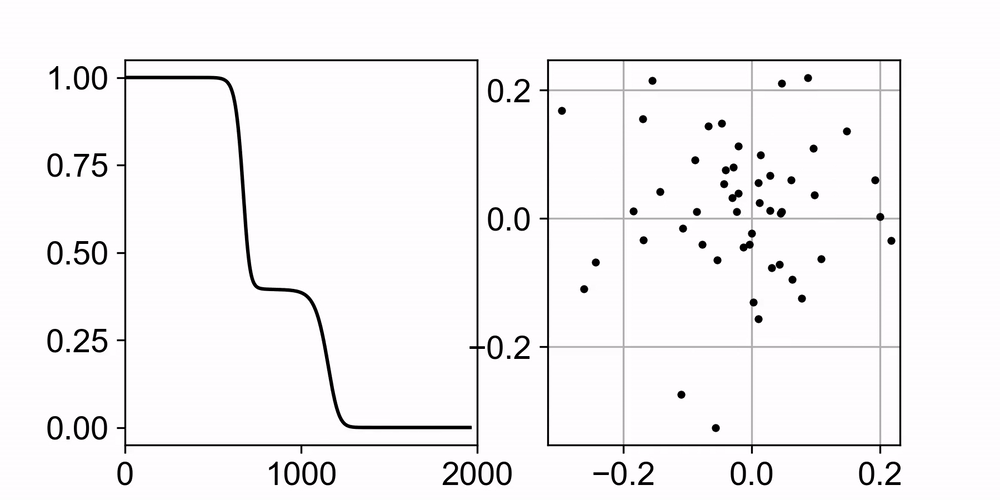
Neural networks trained with gradient descent often learn solutions of increasing complexity over time, a phenomenon known as simplicity bias. Despite being widely observed across architectures, existing theoretical treatments lack a unifying framework. We present a theoretical framework that explains a simplicity bias arising from saddle-to-saddle learning dynamics for a general class of neural networks, incorporating fully-connected, convolutional, and attention-based architectures. Here, simple means expressible with few hidden units, i.e., hidden neurons, convolutional kernels, or attention heads. Specifically, we show that linear networks learn solutions of increasing rank, ReLU networks learn solutions with an increasing number of kinks, convolutional networks learn solutions with an increasing number of convolutional kernels, and self-attention models learn solutions with an increasing number of attention heads. By analyzing fixed points, invariant manifolds, and dynamics of gradient descent learning, we show that saddle-to-saddle dynamics operates by iteratively evolving near an invariant manifold, approaching a saddle, and switching to another invariant manifold. Our analysis also illuminates the effects of data distribution and initialization on the duration and number of plateaus in learning, dissociating previously confounding factors. Overall, our theory offers a framework for understanding when and why gradient descent progressively learns increasingly complex solutions.

---

Saddle-to-saddle learning dynamics in a variety of network architectures

Type I		Type II		Type III
Linear fully-connected network		ReLU fully-connected network		Linear self-attention
Linear convolutional network		ReLU convolutional network		Quadratic network

Across the six two-layer networks with different architectures, gradient descent learning all exhibits saddle-to-saddle dynamics. During the intermediate plateau, the network visits a saddle in weight space, at which it implements a solution expressible by the architecture with a single unit. At the end of learning, the network converges to a stable fixed point, at which it implements a solution expressible with two units. The fixed points visited during learning fall into three different categories described in Theorem 1 of the paper:

• Type I: the rank of the weights increases during learning.
• Type II: the number of rays of proportional weights increases during learning.
• Type III: the number of hidden units with nonzero weights increases during learning.

---

This webpage template is borrowed from here.